自分の実力を把握して、効果的に学習しよう！
SPI学習の
ステップ別攻略法
SPIの学習を「ステップ1」～「ステップ5」の5段階に分け、各段階であなたに必要なSPI学習のポイントをまとめました。
現在の実力と転職を目指す企業によって、学習のスタート地点～到達すべき地点が異なります。効率よく学び、必要な点数をコンスタントに獲得できるようにして、本番に備えましょう。
-
学習ステップ1
SPIの構造を理解するところからスタートします。
-
学習ステップ2
SPI非言語で失敗する人の共通点は、「割合、％の計算」がわかっているようで、実はわかっていないことにあります。
-
学習ステップ3
SPI非言語段階5（中級レベル）の最新の出題傾向とその対策からスタートします。
-
学習ステップ4
SPI非言語段階6（上級レベル）の最新の出題傾向とその対策からスタートします。
-
学習ステップ5
身につけた実力が発揮できるように、独自の試験形態に慣れるところからスタートします。
学習ステップ
SPIの構造を理解するところから
スタートします。
試験形態
SPIは大きく3つに区分されます。
PCでの受検が主流ですから、PCを使った試験に慣れておくことが合格の重要ポイントです
（SPI マークシートの模擬試験経験は、役に立たないと理解しておきましょう）。
| テストセンター型（テストセンター） | 1番多く利用されています。PCで受検します。 |
|---|---|
| 自宅受検型（WEBテスティング） | 2番目に利用されています。PCで受検します。 |
| ペーパー型（マークシート） | ほぼ使われていません。紙のマークシートで受検します。 |
試験の出題範囲
テストセンター、WEBテスティング、マークシートで、出題範囲はそれぞれ異なります。
特にマークシートは、他のテストと出題範囲が大きく異なります。
どのタイプのSPI試験をターゲットにするかを事前に決めておくことが、効率の良い学習のカギとなります。
独特な試験形態
テストセンターの試験画面を理解しましょう。
（WEBテスティングも画面はほぼ同様）
試験画面の説明を見る
SPIテストの仕組み
SPIのテストセンターは独自の出題方式を採用しています。
- オーソドックスな問題（段階3 or 4程度）からスタートし、解答の正誤状況に応じて出題する問題の難易度が変化します。
- 試験時間終了時にどのステージにいるかが試験の結果となります。
- 制限時間前でも受検者の実力を判断できた時点で終了します。
- 正解数が得点になる訳ではありません。
※模擬テストでは7段階評価ではなく、3未満・3・4・5・6以上 の5段階評価となります。
学習のポイント
言語（国語）は、日本語の理解力（読解力）を試す問題ですので、意味がまったくわからないということはまずないでしょう。
点数も、他の受検生とそれほど大きな差は開きません。また、短期間の学習で読解力を高めることは困難です。
非言語（算数）は、受検生によって得点差が大きく開きます。短期の学習でも成績を大きく伸ばすことができます。
したがって、非言語の学習を中心に学習することが効果的です。
学習ステップ
SPI非言語で失敗する人の共通点
SPI非言語で必須の「割合、％の計算」がわかっているようで、実はわかっていないことが原因にあります。
割合、％の計算ができない原因を理解しましょう。
算数の問題は大きく3つに
分けることができます。
-
問題1
720g のケーキを3等分しました。
Bさんはその2切れを持ち帰り、4人で等しく分けて食べました。
Bさんが食べたのは何gか？答→ 120g
-
問題2
ケーキを3等分しました。
Bさんはその2切れを持ち帰り、4人で等しく分けて食べました。
Bさんが食べた量は元のケーキのどれだけに相当するか？答→ 1/6
-
問題3
ケーキを3等分しました。
Bさんはその1切れを持ち帰りました。持って帰ったケーキは240g でした。3等分する前のケーキは何ｇか？答→ 720g
問題1では、ケーキの重さは720ｇと具体的な量が書かれています。
これは具体的な量を計算する問題で、小学校の低学年の算数です。
問題2は、ケーキの重さの具体的な量が書かれていません。
ですからケーキの重さを1とした割合いの計算をしています。
これは具体的な量ではなく抽象的な量を計算する問題で、小学校の高学年の算数です。
（分数、割合、％は具体的な量ではなく、抽象的な量です。）
問題3では、具体的な量と抽象的な量が両方含まれています。
割合、％の計算ができない原因は、この「抽象的な量」を頭の中で整理する方法が身についていないからです。
「抽象的な量」がどこまで理解できているか、簡単なチェックをしてみましょう。
次の6問にトライしてください。
-
問題1
定価600円の商品を15個売りました。
売上金額を求めなさい。答えを見る
答→ 9,000円
-
問題2
400円の商品がいくつか売れました。売上は4,400円でした。
いくつ売れたでしょう。答えを見る
答→ 11個
-
問題3
ある商品が20個売れました。売上は4,000円でした。
価格はいくらでしょう。答えを見る
答→ 200円
-
問題4
定価1,000円の商品を25%値引きしました。
値引き額を求めなさい答えを見る
答→ 250円
-
問題5
定価2,000円の商品を値引きしました。値引き額は300円です。
値引き率を求めなさい。答えを見る
答→ 15％
-
問題6
ある商品を12.5%値引きしました。値引き額は150円です。
値引き前の価格を求めなさい。答えを見る
答→ 1,200円
1～3は具体的な量の計算でした。
4～6は抽象的な量と具体的な量が両方含まれる問題です。
大学3年生の問題4の平均正解率：70％
大学3年生の問題5の平均正解率：50％
大学3年生の問題6の平均正解率：30％ です。
「具体的な量は計算できるが、抽象的な量が含まれると、正解率が一気にダウンする。」
これがSPIの受検者の実態です。
抽象的な量の計算をマスターすることが、SPI非言語得点アップの最重要ポイントです。
抽象的な量の計算は、実は小学校で習った比例計算です。
比例計算の例（やってみましょう）
-
問題1
同じ大きさのペットボトルが5つあります。この5つのペットボトルに溢れるまで水を入れると合計で1,950ml入りました。
溢れるまで水を入れた5つのペットボトルから2本を持って外出しました。
外出に持って行った水は合計で何mlでしょうか。答えを見る
答→ 780ml
-
問題2
同じ大きさのペットボトルが数本あります。全てのペットボトルに溢れるまで水を入れると合計で1,950ml入りました。ペットボトル全体の本数から40%に相当する本数のペットボトルを持って外出しました。外出に持って行った水は合計で何mlでしょうか。
答えを見る
答→ 780ml
1は純粋な比例計算です。
2は抽象的な量の計算です。
1と2の解き方が同じであることを解説します。
（解き方が同じなので、1が正解した人は、2も正解できるようになります。）
-
問題1
このように2本の矢印を書いて、問題文中の数字を記入します。求める2本の水の量を？で記入します。
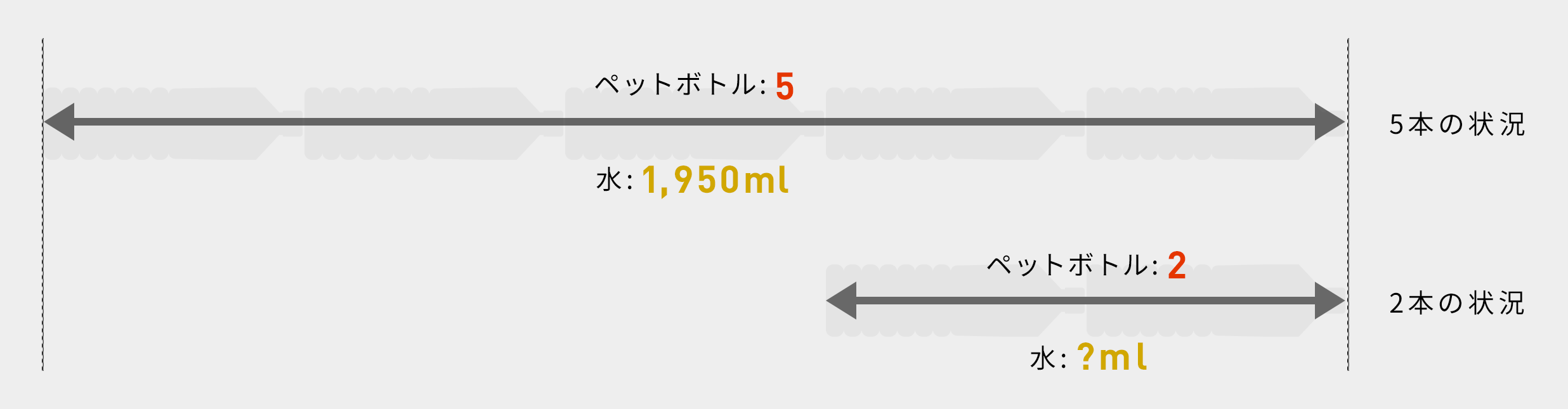
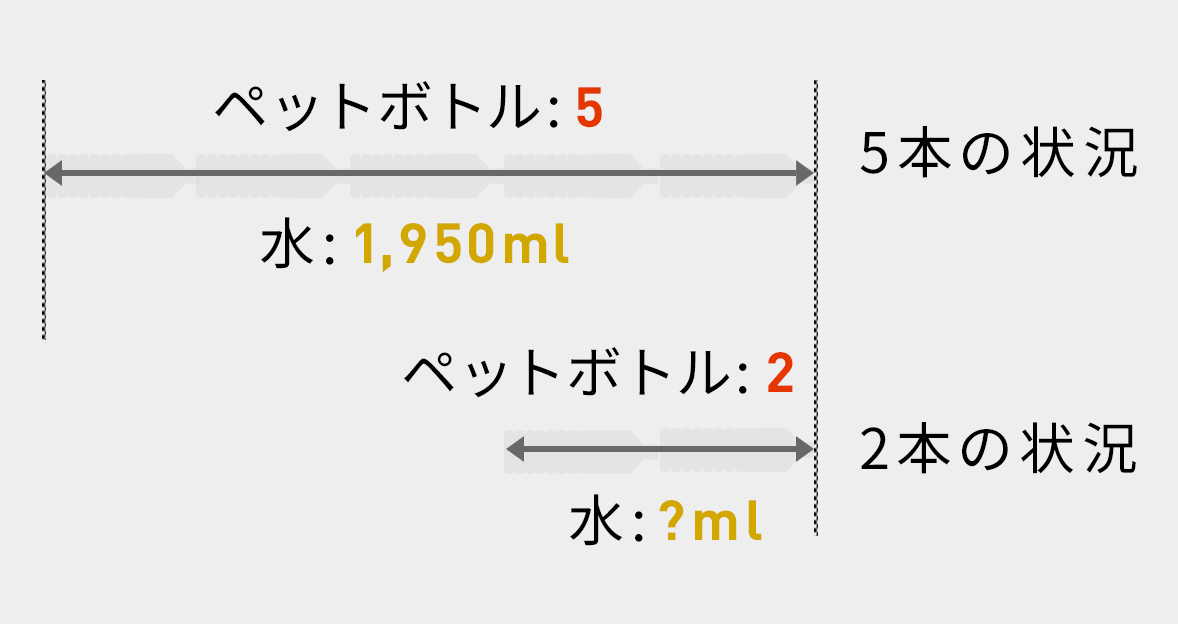
比例式を書きます。
大きい矢印の上：小さい矢印の上 = 大きい矢印の下：小さい矢印の下
5:2 = 1,950:?
比例式を変形します。学校で習いました。比例式の外側同士をかけた値は比例式の内側同士をかけた値と同じ
5×？ = 2×1,950
? = 2×1,950÷5 = 780
-
問題2
2の問題も同じ図を描きます。
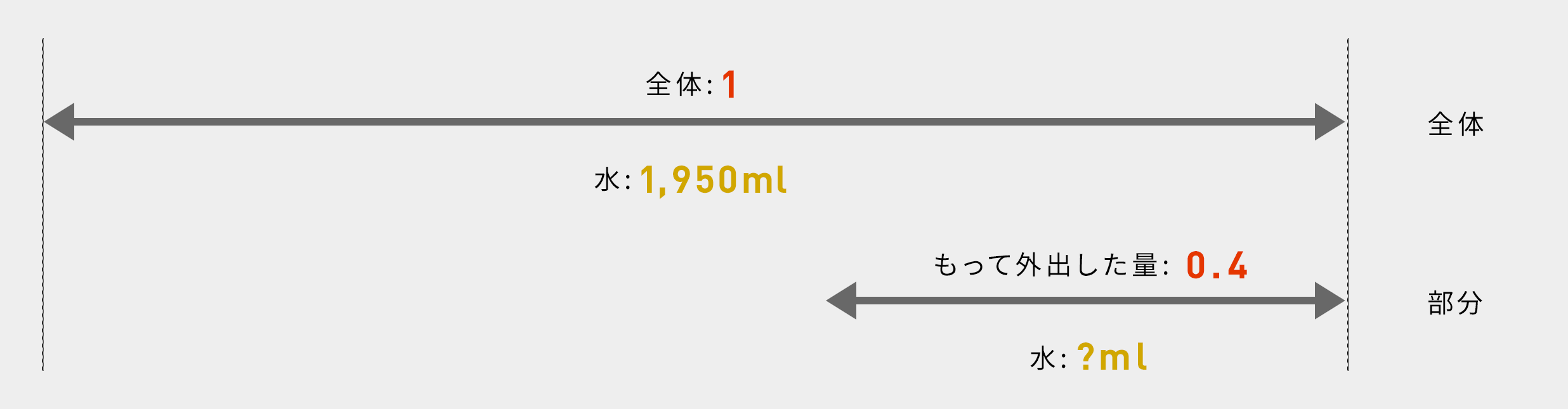
ペットボトルの具体的な量が書かれていないので、全体を1、持って外出した量を0.4と抽象的な量で表現します。
ですから大きい矢印の上が1、小さい矢印の上が0.4になります。
後は、先ほどと同じ比例計算です。
大きい矢印の上：小さい矢印の上 = 大きい矢印の下：小さい矢印の下
1:0.4 = 1,950:?
比例式を変形します。学校で習いました。比例式の外側同士をかけた値は比例式の内側同士をかけた値と同じ
? = 0.4×1,950
? = 0.4×1,950 = 780
2番の％の問題が1番の比例と同じ方法で答えを求めることができました。
％の問題はこの図を描くことで、解けます。
％だけではなく、速度、濃度、人口密度の計算も同じ図を描くことで解けます。
（速度、濃度、人口密度もベースは比例計算なのです。）
SPI非言語の出題分野の内、以下の分野はこの比例計算の方法で解くことができます。
料金の割引
損益算
速度
分割払い
割合・比
図表の読取
確率
学習のポイント
分野ごとで使う公式を覚える必要はありません。
比例計算をマスターするだけで、SPIの多くの問題を解くことができます。
（問題のタイプにより図にアレンジは必要です。）
学習ステップ
SPI非言語段階5（中級レベル）の最新の出題傾向とその対策からスタートします。
段階5の最新の出題傾向は、すべて抽象的な量の表です。
（抽象的な量の説明はこちら）
-
問題1
ある市に存在する4つの大学Ｐ、Ｑ、Ｒ、Ｓで調査を行い、通学に主として利用した交通手段を1つだけあげてもらった。表1は、回答結果にもとづいて、大学ごとに利用した交通手段の割合を示したものである。また表2は、大学ごとの回答者数が回答者数全体に占める割合を示している。
Ｑ大学で「電車」と答えた人は、Ｑ大学での回答者数の何％か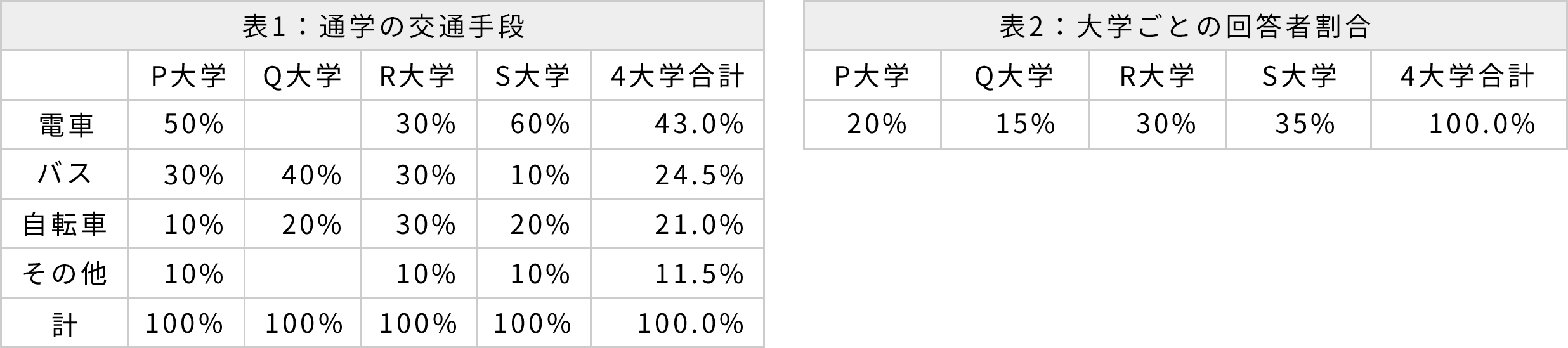
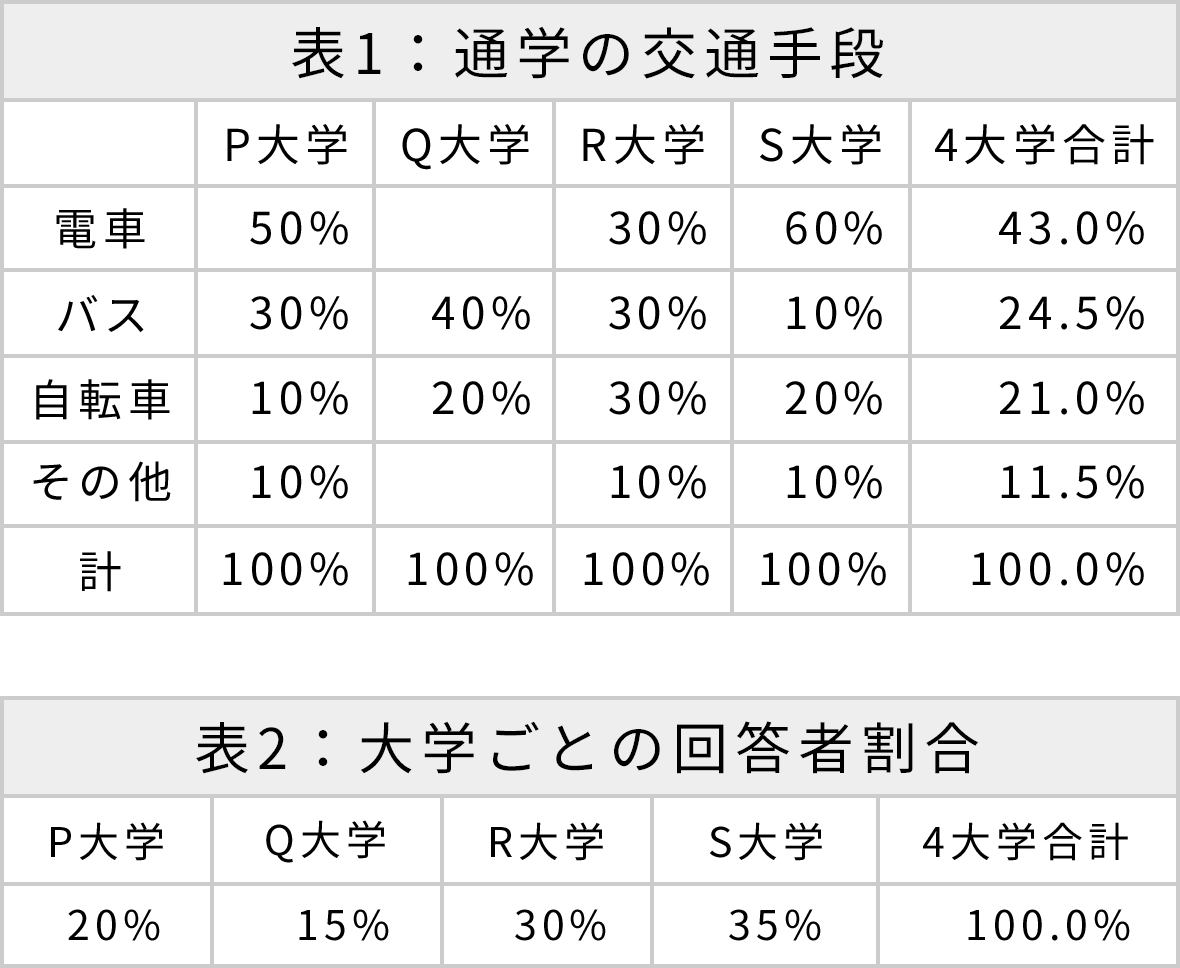
答→ 20％
短時間で簡単に解答するテクニックを解説します。
この問題の特徴は以下の通りです。
・問題文中に具体的な量がない。
・問題文中の数字はすべて抽象的な量。
学習のポイント
問題文中に具体的な量の記載がないので、仮に具体的な量を設定することがコツです。
回答者全員 の具体的な量（回答者数）を1,000人 と設定します。（2,000人でも、100,000人でも同じです。）
そうすると下記の計算ができます。
- 4大学合計で電車と答えた人 ：430人 1,000人 × 0.43
-
Ｐ大学で電車と答えた人
：100人
1,000人 ×0.2（P大学の回答者割合）
×0.5（P大学の電車利用率） -
Ｒ大学で電車と答えた人
：90人
1,000人 ×0.3（R大学の回答者割合）
×0.3（R大学の電車利用率） -
Ｓ大学で電車と答えた人
：210人
1,000人×0.35（S大学の回答者割合）
×0.6（S大学の電車利用率） - Ｑ大学で電車と答えた人 ：30人 430 – 100 – 90 – 210
- Ｑ大学の回答者 ：150人 1,000人 ×0.15
Ｑ大学で電車と答えた人（30人）はQ大学での回答者数（150人）の20％
すべて具体的な量の計算です。
小学校低学年の算数のレベルです。
この問題を抽象的な量のまま、計算すると時間がかかりますし、計算間違いを起こす危険もあります。
テストセンターの試験は電卓を使うことができません。
すべて筆算で計算します。
具体的な量のほうが、筆算の計算は簡単です。
学習ステップ
SPI非言語段階6（上級レベル）の最新の出題傾向とその対策からスタートします。
段階6は主に推論分野の問題が出題されます。
推論は旧タイプと新タイプの2種類あります。
最近の出題傾向は最初、旧タイプの推論が出題され、出題された旧タイプの推論で一定以上の正解があると、新タイプの推論が出題されるようです。
-
旧タイプの推論
Ｐ市、Ｑ市、Ｒ市の人口密度（面積1平方㎞あたりの人口）を表に示してある。
Ｐ市とＲ市の面積は等しく、Ｑ市の面積はＰ市の2倍である。
つぎの推論ア、イの正誤について正しいものはどれか。
次のＡ～Ｉの中から1つ選びなさい。
- アＱ市の人口はＲ市の人口より少ない
- イＱ市とＲ市を合わせた地域の人口密度は175である
- Ａ.アもイも正しい
- Ｂ.アは正しいが、イはどちらとも決まらない
- Ｃ.アは正しいが、イは誤り
- Ｄ.アはどちらとも決まらないが、イは正しい
- Ｅ.アはどちらとも決まらないが、イは誤り
- Ｆ.アは誤りだが、イは正しい
- Ｇ.アは誤りだが、イはどちらとも決まらない
- Ｈ.アもイもどちらとも決まらない
- Ｉ.アもイも誤り
選択肢から正しいものを1つ選びます。
-
新タイプの推論
Ｐ、Ｑ、Ｒ、Ｓの生徒は合計で 8匹の犬を飼っている。
- Ⅰ）Ｐの他にもう一人同じ数の犬を飼っている人がいる。
- Ⅱ）Ｑの他にもう一人同じ数の犬を飼っている人がいる。
- Ⅲ）Ｒは 3匹の犬を飼っている。
Ｓが飼っている犬は何匹か。考えられる数字をすべて選べ。
- Ａ.1匹
- Ｂ.2匹
- Ｃ.3匹
- Ｄ.4匹
- Ｅ.5匹
- Ｆ.6匹
選択肢から正しいものを全て選びます。
学習のポイント
SPI対策の参考書の多くは、旧タイプの推論の解き方しか説明していません。
新タイプの推論の対策も重要です。
学習ステップ
段階6以上の実力を持った受検者への出題パターン
※優良企業から内定を受けた学生からのヒアリングをもとに、まとめたものです。
- 計算問題の出題は試験開始から4～5問のみ
- 5問目、6問目からは計算問題ではなく、推論の問題が出題
- 推論も最初は「選択肢から正しいものを1つ選ぶタイプ」からスタート
- 「選択肢から正しいものを1つ選ぶタイプ」が2～3問出題
- その後、「選択肢から正しいものを全て選ぶタイプ」が出題
ここから下記の事が読み取れます。
-
試験は大きく前半の計算問題のフェーズ（段階4、段階5レベルの出題）と後半の推論のフェーズ（段階6レベルの出題）に分けることができます。
-
後半の推論でも4問以上の正解が求められます。
-
優秀な結果を残した受検生は前半の計算問題のフェーズを4～5問で終わらせています。
学習のポイント
段階6達成のコツ
計算問題よりも、推論の問題の方が1問あたりの正解までに時間を要します。
その推論で4問程度の正解を得るためには、試験開始から早いタイミングで推論が出題される状態を作らないと時間不足の結果になることを多くの受検生は理解できていません。
段階6達成のためには、推論の問題を解く力はもちろん必要ですが、推論が出題される以前の計算問題を短時間で完了する力も必要です。
段階4、段階5に時間をかけないために。
- テストセンターは電卓が使えません。全て筆算ですが、筆算に慣れて勘を取り戻しておきましょう。
- 段階5の全て抽象的な量の計算を短時間で簡単に解くテクニックを身につけておきましょう。（学習ステップ3参照）
- 集合の出題頻度は高いです。集合もカルノー表を使う短時間で簡単に解くテクニックを身につけておきましょう。
